Bates Model and Cliquet Pricing in Numerix

Recently, we added the Bates stochastic volatility jump-diffusion model to the Numerix CrossAsset model library. This is the market standard model for pricing exotic options that depend heavily on the forward skew, such as cliquets and other forward-starting trades.

For these types of options, the classic Black-Scholes model [1] is inadequate, because it implies constant volatility. The Heston model [2] extended the Black-Scholes model with a stochastic volatility process, providing close agreement with the implied volatility surface and realistic dynamics for the smile. However, no stochastic volatility model—including the widely used Heston model—can fit short-dated skew without incorporating the possibility of jumps in the underlying asset.

The Bates model [3] does just that, extending the Heston model by explicitly adding a jump-diffusion process. This is more consistent with empirical evidence, providing better calibration to the short-term skew and more realistic forward-skew dynamics.

Numerix Implementation

Numerix supports the classic Bates model, as well as an enhanced version that provides a better fit to market volatilities (more information is available by contacting Numerix sales). It includes support for:

• Monte Carlo simulation, as well as finite difference methods (used for weakly path-dependent instruments such as barrier options or American options)
• The option to draw jumps from either log-normal (Merton) or double-exponential (Kou) distribution
• Use of Bates as an equity component in the Numerix hybrid model framework for pricing structured products with underlyings from multiple asset classes

Applying the Bates Model to Cliquet Options

One of the uses of the Bates model is in pricing cliquets, or “ratchet options.” These are essentially a series of forward-start options, in which the strike price is reset to the current value of the underlying at each option expiration. The cliquet has become increasingly popular as way for sophisticated investors to trade on volatility assumptions. They’re also used in many retail structured products that give investors a lower-risk way to participate in equity and bond markets.

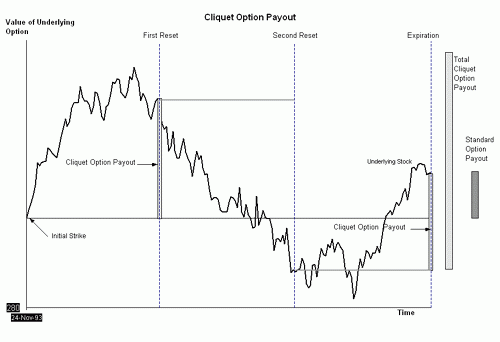
The Bates model is well-suited to cliquets, because of the model’s ability to accurately calibrate to the forward volatility smile and account for frequent strike-price resets.

To illustrate, we calculated a standard cliquet contract using the Black-Scholes model, Dupire (local volatility) model, Heston model and Bates model. Only the Bates model produced a result within range of the market-observed price due to its ability to capture jump events and accurately describe implied volatility dynamics. The price increase going from Black-Scholes to Heston is a result of the stochastic volatility increasing in the forward skew, while jumps in the Bates model increases it even further.

Trade: 1-year cliquet on SPX Index with 1-month resets and a local cap of 3%, trading on 24-Apr-2009 and expiring on 26-Apr-2010.

Prices quoted are for demonstration purposes only and should not to be used for trading.

The use of the Bates model gets you in the door to the cliquet market—but to use cliquets effectively, you should be able to tailor them to investors’ needs…

The Numerix Advantage: Customization

One of the advantages of Numerix is flexibility—allowing you to quickly and easily customize trades using a transparent deal-definition framework. For example, floors and caps can be added to keep the contract value affordable, and the strike reset can be modified to a set percentage above or below the underlier.

And that’s just the beginning. Using our versatile payoff scripting language, it’s possible to define ANY conceivable payoff, allowing users to easily prototype new variations on the cliquet—allowing them to stay ahead of the market and giving them a competitive advantage.

To learn more about how to get the Bates model for your systems, contact Numerix sales.

References

[1] Black, Fischer; Myron Scholes, 1973. The Pricing of Options and Corporate Liabilities. Journal of Political Economy, Vol. 8, No. 3, pp. 637–654.

[2] Heston, Steven L., 1993. A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options. The Review of Financial Studies, 1993, Vol. 6, No. 2, pp. 327–343.

[3] Bates, David S., 1996. Jumps and Stochastic Volatility: Exchange Rate Processes Implicit in Deutsche Mark Options. Review of Financial Studies, Vol. 9 No. 1, pp 69-107.